Until very recently, Google Maps gave street names in Taiwan in Tongyong Pinyin — most of the time, at least. This was the case even for Taipei, which most definitely has long used Hanyu Pinyin, not Tongyong Pinyin. The romanization on Google Maps was really a hodgepodge in the maps of Taiwan. And it’s still kind of a mess; but now it’s at least more consistent — and more consistent in Hanyu Pinyin.
First the good. In Google Maps:
- Hanyu Pinyin, not Tongyong Pinyin, is now used for street names throughout Taiwan
- Tone marks are indicated. (Previous maps with Tongyong did not indicate tones.)
Now the bad, and unfortunately there’s a lot of it and it’s very bad indeed:
- The Hanyu Pinyin is given as Bro Ken Syl La Bles. (Terrible! Also, this is a new style for Google Maps. Street names in Tongyong were styled properly: e.g., Minsheng, not Min Sheng.)
- The names of MRT stations remain incorrectly presented. For example, what is referred to in all MRT stations and on all MRT maps as “NTU Hospital” is instead referred to in broken Pinyin as “Tái Dà Yī Yuàn” (in proper Pinyin this would be Tái-Dà Yīyuàn); and “Xindian City Hall” (or “Office” — bleah) is marked as Xīn Diàn Shì Gōng Suǒ (in proper Pinyin: “Xīndiàn Shìgōngsuǒ” or perhaps “Xīndiàn Shì Gōngsuǒ“). Most but not all MRT stations were already this incorrect way (in Hanyu Pinyin rather than Tongyong) in Google Maps.
- Errors in romanization point to sloppy conversions. For example, an MRT station in Banqiao is labeled Xīn Bù rather than as Xīnpǔ. (埔 is one of those many Chinese characters with multiple Mandarin pronunciations.)
- Tongyong Pinyin is still used in the names of most cities and townships (e.g., Banciao, not Banqiao).
Screenshot from earlier this evening, showing that Tongyong Pinyin is still being used in Google Maps for some city and district names (e.g., Gueishan, Sinjhuang, Banciao, Jhonghe, Sindian, and Jhongjheng rather than Hanyu Pinyin’s Guishan, Xinzhuang, Banqiao, Zhonghe, Xindian, and Zhongzheng, respectively).
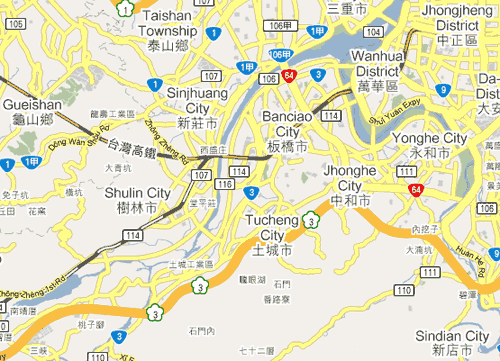
I don’t have any old screenshots of my own available at the moment, so for now I’ll refer you to an image that Fili used in an old post of his. Compare that with this screenshot I took a few minutes ago from Google Maps of the same section of Tainan:
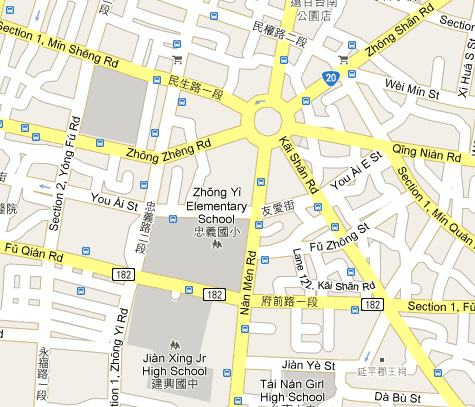
Note especially how the name of the junior high school is presented.
- Previously “Jian Xing Junior High School”.
- Now “Jiàn Xìng Jr High School”.
This is typical of how in old maps some things were labeled (poorly) in Hanyu Pinyin. (Words, not bro ken syl la bles, are the basis for Pinyin orthography. This is a big deal, not a minor error.) And now such places are still labeled poorly in Hanyu Pinyin, but with the addition of tone marks.
I’d like to return to the point earlier on sloppy conversions. Surprisingly, 成都路 is given as “Chéng Doū Road” rather than as “Chéngdū Road“.
![screenshot from Google Maps of 'Cheng Dou [sic] Rd', near Taipei's Ximending](https://pinyin.info/news/news_photos/2009/11/cheng_dou_road.gif)
Although “Xinpu” might not be the sort of name to be contained in some romanization databases, there is nothing in the least obscure about Chengdu, the name of a city of some 11 million people. Google Translate certainly knows the right thing to do with 成都路:
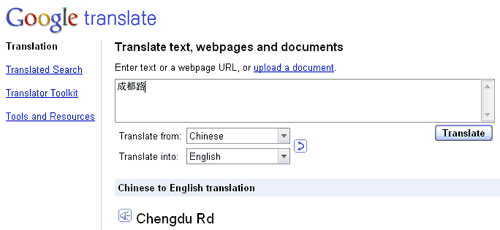
But Google Maps doesn’t get this simple point right, which likely points to outsourcing. Why would Google do this? And why wouldn’t it ensure that a better job was done? Because, really, so far the long-overdue conversion to Hanyu Pinyin in Google Maps for Taiwan is something of a botch.

Sloppily is right! My former address (Yunong Lu) comes out as Yù Agricultural Rd.
Imagine trying to explain that to a taxi driver!
If it’s ever going to be entirely consistent, Google would have to switch to Hanyu pinyin for city names too, i.e. Taibei, Taizhong, Gaoxiong, etc. At present, they have for example “Tai Zhong Gang Road”, which is a road in Taichung City!
They would probably label Taipei as “Tai North City” and Tainan “Tai South City” based on what they did to Zhinan Road in Maokong :)
Yeah, Google is using some weird romanisation… A while ago when I zoomed into a part of Gaoxiong I was surprised to see lots of names in (sometimes “strange”) Hanyu Pinyin – but along Tongyong, and the city name itself was of course still W/G…
A screenshot:
http://dl7und.net/files/img/gxgm2.jpg
Pingback: Pinyin news » Google Translate’s new Pinyin function sucks
The government has decided to use Hanyu Pinyin as the standard of romanization, except those are popular around the world (e.g. Taipei, Kaohsiung). The traditional railway system has started changing all the romanizations around Taiwan (that costs a lot $). But the high speed railway has not start this process. Therefore in some stations, you’ll see 3 different romanizations (including WG).
Though, currently only the signs on the road in Taipei City are in (CamelCased) Hanyu Pinyin ;)
fix:
Taiwan railway system has started changing all the romanizations
around Taiwanof all the railway stations.Google bought out a start-up in Boulder, CO (where I’m from), and one of my friends who had been at the start-up is working for Google maps as a result. She said they just use the government data.
Rather than wading into what is unfortunately a political debate, Google just populates their database with the data given to them. It’s a pretty rational approach, all things considered.
Out of curiosity why do you care so much about syllables being split up? Non-standard spellings definitely make things difficult for the character illiterate users of the map, as do missing tone marks to some extent. I can recall numerous times I had difficulties communicating place names when I was a beginning level student and saw “g?tíng” romanized as “kuting” or “zh?ngsh?n” as “chungshan”.
Not merging syllables, on the other hand, hardly poses any hardship at all. Or at least it never did for me.
I just tried searching for a few things on Google Maps and this highlights one of the problems with incorrect word parsing. For an example, try searching for “Nanjing East Road Taipei City” and “Nan Jing East Road Taipei City”.
Google went for a quick and easy solution rather than doing the job properly. It is not that big a task to compile a database of street and place names, especially when many names are repeated across Taiwan. I hope that Google recognise this problem and fix it.
Google bought out a start-up in Boulder, CO (where I’m from), and one of my friends who had been at the start-up is working for Google maps as a result. She said they just use the government data.
Rather than wading into what is unfortunately a political debate, Google just populates their database with the data given to them. It’s a pretty rational approach, all things considered.
Heaven knows I have little faith in the ability of the government here to handle romanization correctly. But I very much doubt that the forms used in Google Maps and Google Translate’s romanizer came from the government of Taiwan. Here are some of the reasons:
First, the orthography does not correspond to any form called for by the government. The Ministry of Education’s rules, which serve as the basis for the central government’s, are quite clear that the style is “Zhongshan” not “Zhong Shan.”
Second, the government rarely if ever uses tone marks; in fact, until late last year the government’s rules on romanization specifically forbade the use of tone marks. (I successfully argued for the removal of this foolish restriction.)
Third, the government may be chabuduo about a lot; but it does know how to spell “Chengdu.”
Fourth, the forms on Google do not correspond to the forms put out by the government.
Fifth, Google is using broken Hanyu Pinyin for things that the government calls for English or traditional spellings for. For example, look at Google Maps for the Taipei MRT system. What is normally referred to as “Taipei Main Station” is labeled by Google as “Tái B?i,” the “Taipei Zoo” is labeled “Dòng Wù Yuán,” etc.
Sixth, what was previously used Google Maps — a bizarre mix of Tongyong (even in Taipei), broken Hanyu Pinyin, and mistakes — certainly corresponded in no way to government policy here, either at the municipal or national level.
Seventh, Google is using Tongyong rather than Hanyu forms for names of many cities, townships, and districts. This is certainly not in accord with government policy.
Out of curiosity why do you care so much about syllables being split up? Non-standard spellings definitely make things difficult for the character illiterate users of the map, as do missing tone marks to some extent. I can recall numerous times I had difficulties communicating place names when I was a beginning level student and saw “g?tíng” romanized as “kuting” or “zh?ngsh?n” as “chungshan”.
Not merging syllables, on the other hand, hardly poses any hardship at all. Or at least it never did for me.
Does Google routinely fragment words into individual syllables in English, French, German, Turkish, Russian, Greek, Swahili, Hindu, Cherokee, etc.? Do you? Does anyone? Why would they? There’s no more call for that to happen with Mandarin written with an alphabet than with any other language written with an alphabet. It simply makes everything less clear.
I wasn’t speaking about Google Translate. It draws from a very large corpus of bilingual text and works differently. However, I’m 100% certain that as of a few months ago, Google Maps had not created its Taiwan data internally. It was using street and location names taken from an official source.
The result at that time was a very broken system with a variety of spelling systems all mixed together. A number of people, including myself gave feedback suggesting that they use standard hanyu spelling and tone marks. I believe the current maps reflect that feedback.
That said, they still rely on an algorithmic solution for obvious reasons. They’re likely using government data (but the Chinese language data now) and converting it to pinyin. The conversion is a bit naive, but it’s a huge improvement from what was on the maps this summer. I’m sure it will gradually be improved to better distinguish ???. If you like, I can ask for you and verify where the current street name data is coming from.
Google routinely follows the conventions of the whatever language markets they’re entering to the best of their ability using whatever resources they’ve allotted. So, no. Of course they don’t break the words of European languages into syllables. Parsing conventions for a barely spoken polysynthetic language like Cherokee with a rarely used syllabary probably isn’t a very high priority for Google now, either.
Why would they parse pinyin as separate syllables? That answer is simple. Literally billions of books are written with pinyin parsed in the standard Chinese fashion and tens of millions of Chinese children own and are in the process of learning from books like this right now. If people truly had a hard time reading pinyin because of spacing conventions, there would probably be a sizable market of books written with English-style spacing to cater to those people. To the best of my knowledge, there isn’t. Thus, not only would such an approach be non-standard, but Google would also lack the corpus it needed to create an effective converter.
The example showing syllable transcription does have one hugely important aspect (which Google doesn’t), which is that it shows neutral tones:
http://image.wangchao.net.cn/product/2/1247494564141.jpg
Also so many streets like:
ChongDeShi 3rd St when they mean ChongDe 13th St
Pingback: Pinyin news » Going south with official Taiwan map
Pingback: Pinyin news » Banqiao — the Xinbei ways
Gentlemen, Google™ Maps is actually composed of several different
currently conflicting datasets, as you can see as we switch the “z=”
zoom paramater,
http://maps.google.com/maps/api/staticmap?sensor=false¢er=24.999184,121.463694&size=222×222&zoom=16
http://maps.google.com/maps/api/staticmap?sensor=false¢er=24.999184,121.463694&size=222×222&zoom=12
( “z=” in http://mapki.com/wiki/Google_Map_Parameters
“zoom=” in http://code.google.com/apis/maps/documentation/staticmaps/ )
Pingback: Pinyin news » Bing Maps for Taiwan
Pingback: Pinyin news » Google improves its maps of Taiwan